One minute
Week1032_share
ARTS - Share 补2019.2.13
基础的重要性
现代计算机的存储结构
现代计算机大多采用冯诺依曼机构,主要分为核心计算中央处理器CPU,内存,作为临时存储数据的模块,硬盘,永久存储数据的地方,还有数据总线,负责之间数据传输通信。
我们与计算机交互,其实就是把数据交给CPU处理,然后结果返回。中间涉及到数据存储、传输、读取,也就是输入输出,简称IO(input output)。实现这个过程的实体就是CPU、内存、硬盘。速度上CPU>内存»硬盘。 我们的目标是用尽可能少的资源(计算资源、时间资源、空间存储资源)得到尽可能多的结果。
由于目前经常是CPU处理性能强大,我们经常优化点就在磁盘(硬盘)IO,和内存存取计算这块,为了实现目标,落到实地就是尽可能的减少磁盘IO,尽可能减少内存开销,和尽可能少的计算。于是出现了各种数据结构,就是为了在不同场景下最大化的利用资源达到目的。数据结构和算法并非凭空产生,都是依托于场景存在,所以学习这类知识不能孤立的只是学习记忆,要尽可能的学习它的适用场景。

数组与链表
数组和链表的产生是基于内存结构的。内存其实就是一块有编号的存储单元。可以想象成有编号的一组柜子。我们程序需要频繁的往这些箱子里放东西,取东西。为了更好的利用这些箱子,提高存取效率,就出现了数据结构和算法,数组和链表就是其中最基础的。
想象一下,我要存十个东西到箱子里,我可以申请编号1-10 的箱子,把东西依次放入,并获得每个东西的箱子号码(内存地址),下次我要取出3号箱子,就直接去3号拿,取出8号的就去8号箱拿。这就是数组结构。我的东西都是连续的,我拿出3,我若需要7就去7号箱子拿,不需要打开4,5,6去看看,但是如果我需要放一个新的东西,按照顺序只能放到3和4之间,于是我就需要把4-10的东西先往后平移一个,在把东西放到4号箱子。这就有点麻烦了,为了放一个,我需要移动4-10 7个箱子。
这时候链表结构就出现了。它的特点就是可能不是非要连续的箱子,我要放十个东西,第一个放入了3号箱,三号箱里还放了第二个东西的箱子编号7,然后第二个东西放入7号箱子,然后7号箱子还放了接下来第三个东西地址,以此类推。这就是链表结构,他的特点就是不需要连续的箱子,只要有空箱子,我的东西就能放进去。目前我们知道我的东西放在 3 -> 7 -> 2 -> 5 ->13 ->9 箱子, 加入我有一个东西需要放在三和四之间,我只需要申请一个空箱子比如 20, 然后把第三个箱子2的下一个箱子指向20, 然后20的下一个箱子指向原来的5就行了,不用移动后面箱子的东西。这就是链表的好处,但是它的坏处就是,假如我只是查找,只能从头开始查,没有数组那种跳着查的方便。
这时候我们已经看到了,数组方便查询,但不方便插入删除,链表方便插入删除,不方便查询。其实这两个结构已经告诉我们使用场景了:在查询多的场景用数组,在插入删除多的场景用链表。
二叉树
数据并非只有数组和链表这样线性的关系,还可能是家谱一样树形关系。典型的是二叉树,每个节点最多有两个孩子节点。二叉树应用场景主要在查询操作和维持相对顺序。
比如一个二叉树的左子树不为空,所有左子树节点均小于根节点的值,右子树不为空的话,所有右子树节点均大于根节点的值。这样的二叉树叫二叉查找树。不用刻意记名字,根据这样特性构建的数,非常方便查询,只要每次比较根节点,小的往左边找,大的往右边找。
二叉树如果只有左子树或者右子树,那么就会退化成了链表结构。为了避免这种情况,或者树太深层级导致查询困难,就产生了各种类型的数,如红黑树、B树之类。
MySQL的B+树
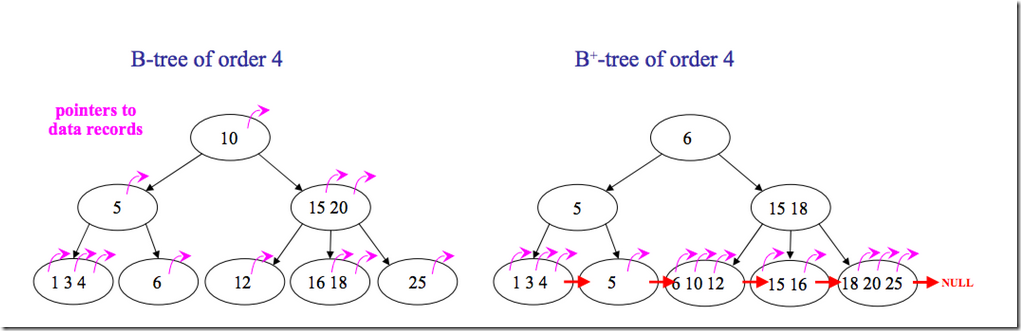
这里说一个典型的mysql索引B+树。我们知道磁盘数据库,要查询数据就要尽可能减少磁盘IO,这样才能加速。于是就有相应场景的B树。它允许每个节点有多于2个的元素,这样可以多存数据,降低数的深度,B+树是在B树的基础上,非叶子节点只有索引功能,数据放在叶子节点上,同时,所有叶子节点构成一个有序链表,这样在limit m, n时候,可以根据找到的一个直接遍历到后边。